Chapitre 3 - Géométrie Plane
- Connaître et utiliser la condition de colinéarité \(x y' - x'y = 0\)
- Utiliser la condition de colinéarité pour obtenir une équation cartésienne de droite
- Déterminer une équation cartésienne à partie d'un vecteur directeur et un point
- Déterminer un vecteur directeur à partir d'une équation cartésienne
- Choisir une décomposition pertinente dans le cadre d'un problème
|
Dans l'ensemble du chapitre, on se placera dans le plan muni du repère orthonormé \((O;\vec{i};\vec{j})\) où on notera \(\vec{u} = \vec{OI}\) et \(\vec{j}=\vec{OJ}\) |

|
IColinéarité de vecteurs
Soient \(A\) et \(B\) deux points du plan. Soit \(\vec{u}\) un vecteur tel que \(\vec{u} = \vec{AB}\)
Le vecteur \(\vec{u}\) son sens, sa direction et sa norme :
- La direction de \(\vec{u}\) est celle de la droite \((AB)\)
- Le sens de \(\vec{u}\) est de \(A\) vers \(B\)
- La norme \(\Vert\vec{u}\Vert\) de \(\vec{u}\) est la longueur \(AB\) : \(\Vert\vec{u}\Vert = AB\)
|
Deux vecteurs sont égaux si ils ont même direction, même sens et même norme.
|

|
|
Deux vecteurs sont colinéaires si ils ont la même direction.
|

|
Propriété Géométrique
Deux vecteurs \(\vec{AB}\) et \(\vec{CD}\) sont colinéaires si et seulement si \((AB)\) et \((CD)\) sont parallèles.
|
Propriété algébrique
Deux vecteurs \(\vec{u}\) et \(\vec{v}\) sont colinéaires si et seulement si il existe un nombre réel \(k\) tel que \(\vec{u} = k \vec{v}\)
|
Formule analytique
Deux vecteurs \(\vec{u} \begin{pmatrix} x \\ y \\ \end{pmatrix}\) et \(\vec{v}\begin{pmatrix} x' \\ y' \\ \end{pmatrix}\) sont colinéaires si et seulement si \(x y' - x' y = 0\)
|
Objectif
On souhaite démontrer que deux vecteurs \(\vec{u} \begin{pmatrix} x \\ y \\ \end{pmatrix}\) et \(\vec{v} \begin{pmatrix} x' \\ y' \\ \end{pmatrix}\) sont colinéaires si et seulement si \(x y' - x' y = 0\)
Stratégie
On doit montrer les deux implications réciproques suivantes :- Si il existe un nombre réel \(k\) tel que \(\vec{u} = k \vec{v}\), alors \(x y' - x' y = 0\)
- Si les coordonnées vérifient \(x y' - x' y = 0\) alors il existe un nombre réel \(k\) à déterminer tel que \(\vec{u} = k \vec{v}\)
Première partie de la preuve
On suppose que \(\vec{u} = k \vec{v}\). Par conséquent : $$ \left\{ \begin{array}{lll} x & = & k x' \\ y & = & k y' \end{array} \right. $$ on vérifie alors la formule : $$ \begin{array}{lll} & & x y' - x' y \\ &=& k x' y' - x' k y' \\ &=& k x'y' - k x'y' \\ &=& 0 \end{array} $$ cqfdDeuxième partie de la preuve
On suppose que les coordonnées des deux vecteurs vérifient \(x y' - x' y = 0\) On essaye de trouver une valeur \(k\) telle que \(\vec{u} = k \vec{v}\).
La formule donne \(x y' = x' y\). Comme on veut isoler \(x\), il y a deux cas :
Cas \(y' \neq 0\) :alors, \(x = \frac{y}{y'} x'\). On pose \(k=\frac{y}{y'}\) On a alors \(x = k x'\) et \(y = k y'\) (car k y'=\frac{y}{y'}y'=y) et donc \(\vec{u} = k \vec{v}\). cqfd |
Cas \(y'= 0\) :alors \(\vec{v}=\begin{pmatrix} x' \\ 0 \\ \end{pmatrix}\) en remplaçant dans la formule, on a \(x' y = 0\) Il y a donc deux possibilités :
|
IIDécomposition d'un vecteur
|
On rappelle la propriété de Chasles :
Soient \(A\), \(B\) et \(C\) des points du plan. Alors : $$\vec{AC} = \vec{AB} + \vec{BC}$$
La propriété de Chasles, a permis de décomposer le vecteur \(\vec{AC}\) comme une somme de deux autres vecteurs.
|

|
Soit \(\vec{u}\) un vecteur de coordonnées \(\begin{pmatrix} x \\ y \\ \end{pmatrix}\) dans le repère \((O;\vec{i};\vec{j})\).
Alors il est possible de décomposer \(\vec{u}\) en fonction de \(\vec{i}\) et \(\vec{j}\) de la manière suivante :
$$\vec{u} = x\vec{i} + y\vec{j}$$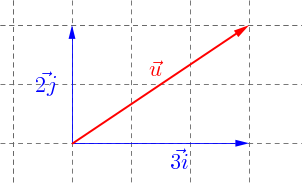
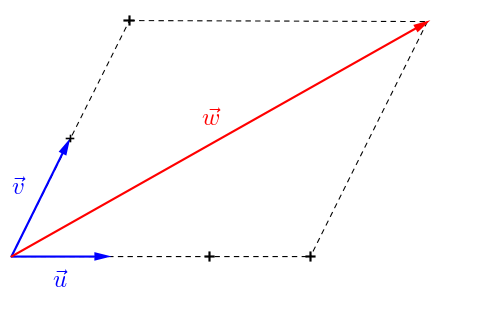
De manière générale, si \(\vec{u}\) et \(\vec{v}\) sont deux vecteurs non colinéaires, on peut décomposer tout vecteur \(\vec{w}\) à partir de \(\vec{u}\) et \(v\) :
Il existe \(x\) et \(y\) deux nombres réels tels que \(\vec{w} = x\vec{u} + y\vec{v}\)
Exercice type : utilisation des propriétés du parallélogramme
|
Soit \(ABCD\) un parallélogramme de centre \(O\). Exprimer \(\vec{AB}\) en fonction de \(\vec{OB}\) et \(\vec{AD}\)
Dans un parallélogramme, \(\vec{DB}=2\vec{OB}\), et comme \(\vec{AB}=\vec{AD} + \vec{DB}\),
on a donc \(\vec{AB}=\vec{AD} + 2\vec{OB}\). |

|
IIIEquation cartésienne d'une droite
|
Toute droite droite du plan \((0;\vec{i},\vec{j})\) a une équation réduite de la forme :
|

|
- Toute droite droite du plan \((0;\vec{i},\vec{j})\) a une équation cartésienne de la forme \(a x + b y + c = 0\) où \(a\), \(b\) et \(c\) sont des nombres réels tels que \(a\) ou \(b\) est non nul.
- Toute équation de la forme \(a x + b y + c = 0\) où \(a\), \(b\) et \(c\) sont des nombres réels tels que \(a\) ou \(b\) est non nul est l'équation d'une droite.
- \(2 x_A - 3 y_A + 7 = 2 \times 1 - 3 \times 3 + 7 = 2 - 9 + 7 =0\) donc \(A \in (D)\)
- \(2 x_B - 3 y_B + 7 = 2 \times (-2) - 3 \times 1 + 7 = -4 - 3 + 7 =0\) donc \(B \in (D)\)
Stratégie
Nous devons démontrer les deux sens du théorème :- On sait que toute droite à une équation réduite. En partant de n'importe quelle équation réduite, on doit trouver une équation cartésienne.
- On doit partir d'une équation cartésienne, et montrer que c'est l'équation d'une droite en trouvant son équation réduite.
Première partie de la preuve
Soit \((D)\) une droite. Il y a deux possibilité : elle a soit une équation réduite de la forme \(y=m x + p\), soit de la forme \(x=k\).
Cas \(y = m x + p\) :alors, \(m x - y + p = 0\). On a une équation cartésienne \(a x + b y + c\) avec \(a = m\), \(b = -1\) et \(c = p\). |
Cas \(x = k\) :alors, \(x - k = 0\). On a une équation cartésienne \(a x + b y + c\) avec \(a = 1\), \(b = 0\) et \(c = -k\). |
Deuxième partie de la preuve
On suppose qu'on a une équation de la forme \(a x + b y + c = 0\) où \(a\), \(b\) et \(c\) sont des nombres réels tels que \(a\) ou \(b\) est non nul.
Cas \(b=0\) :alors, \(a\neq 0\) car \(b\) et \(a\) ne peuvent être tous les deux nuls, et : $$ \begin{array} a x + b &=& 0\\ a x &=& -b\\ x &=& \frac{-b}{a} \text{ } (a\neq 0) \\ \end{array} $$ On a une équation réduite du type \(x = k\) avec \(k = \frac{-b}{a}\), donc une droite verticale. |
Cas \(b\neq 0\) :alors : $$ \begin{array} a x + b y + c &=&0\\ b y & = & -a x - c\\ y &=& \frac{- a x - c}{b} \text{ } (b \neq 0)\\ y &=& \frac{-a}{b} x + \frac{-c}{b} \\ \end{array} $$ On a une équation réduite du type \(y = m x + p\) avec \(m = \frac{-a}{b}\) et \(p=\frac{-c}{b}\). |
Exercice type
Correction
La droite n'est ni horizontale, ni verticale, on va chercher les points qui coupent les axes des abscisses \(A (x_A;0)\) et des ordonnées \(B (0;y_B)\)| Calcul de \(x_A\) : $$ \begin{array}{lll} 2 x_A - 0 + 3 &=& 0\\ x_A &=& \frac{-3}{2} \end{array} $$ Donc \(A (-1,5;0)\) | Calcul de \(y_B\) : $$ \begin{array}{lll} 2 \times 0 - y_B + 3 &=& 0\\ y_B &=& -3 \end{array} $$ Donc \(B (0;-3)\) |
IVVecteur directeur d'une droite
1Généralités
- Une droite à une infinité de vecteurs directeurs, et un vecteur non nul est le vecteur directeur d'une infinité de droites.
- Le vecteur nul est le seul vecteur à n\être le vecteur directeur d'aucune droite.
2D'équation de droite à vecteur directeur
|
Soit \((D)\) une droite dont on considère l'équation réduite :
|

|
Cas \((D):y = m x + p\)
- Soit \(A\) le point de la droite \((D)\) d'abscisse 0 : \(A (0;p)\)
- Soit \(B\) le point de la droite \((D)\) d'abscisse 1 : \(B (1;m+p)\)
On pose \(\vec{u} = \begin{pmatrix} 1 \\ m \\ \end{pmatrix}\). cqfd
Cas \((D):x=k\)
La droite est verticale donc n'importe quel vecteur vertical est directeur. On prend \(\vec{j}\begin{pmatrix} 0 \\ 1 \\ \end{pmatrix}\)Soit \((D)\) une droite d'équation cartésienne \(a x + b y + c = 0\) avec \(a\) ou \(b\) non nul.
Alors le vecteur \(\vec{u}\begin{pmatrix} -b \\ a \\ \end{pmatrix}\) est un vecteur directeur.
Stratégie
On va se ramener au cas des équations réduites et utiliser la propriété précédente :Cas \(b=0\)
L'équation est \(a x+ c =0\) qui se ramène à \(x = \frac{-c}{a}\) (car \(a\neq 0\)).C'est une droite verticale, donc le vecteur \(\vec{u}=\begin{pmatrix} b \\ a \\ \end{pmatrix}\begin{pmatrix} 0 \\ a \\ \end{pmatrix}\) est un vecteur directeur.
Cas \(b\neq 0\)
L'équation réduite devient \(y = \frac{-a}{b} + \frac{-c}{b}\) (on a divisé par \(b\neq 0\))D'après la propriété précédente, on a le vecteur directeur \(\begin{pmatrix} 1 \\ \frac{-a}{b} \\ \end{pmatrix}\)
Or, un vecteur reste directeur si il est multiplié par un nombre réel (car colinéaire). Donc en multipliant par \(-b \neq 0\), on obtient le vecteur directeur : $$\vec{u}=-b\times\begin{pmatrix} 1 \\ \frac{-a}{b} \\ \end{pmatrix}=\begin{pmatrix} -b \\ a \\ \end{pmatrix}$$ cqfd
Exercice type : vérifier le parallélisme de deux droites
- Calculer un vecteur directeur pour chacune des droite.
- Les droites \(D\) et \(D'\) sont-elles parallèles ?
Correction
On applique les formules connues :-
- \(\vec{u}\begin{pmatrix} 1 \\ -2 \\ \end{pmatrix}\) est un vecteur directeur de \((D)\).
- \(\vec{v}\begin{pmatrix} -2 \\ 4 \\ \end{pmatrix}\) est un vecteur directeur de \((D')\).
- Les vecteurs \(\vec{u}\) et \(\vec{v}\) sont colinéaires (on peut utiliser la formule : \(1\times 4 - (-2) \times (-2)=0\) ou remarquer que \(\vec{v}=-2\vec{u}\)), et donc les droites \(D\) et \(D'\) sont parallèles.
3De vecteur directeur à équation de droite
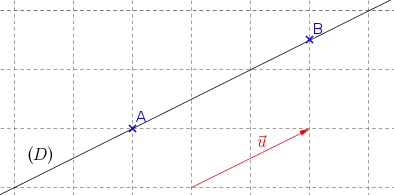
Soit \((D)\) une droite de vecteur directeur non nul \(\vec{u}\begin{pmatrix} \alpha \\ \beta \\ \end{pmatrix}\) passant par un point \(A (x_A;y_A)\). Il est possible de donner son équation cartésienne \(a x + b y + c = 0\) avec \(a\) ou \(b\) non nul, en exprimant \(a\), \(b\) et \(c\) à partir de \(\alpha\), \(\beta\), \(x_A\) et \(y_A\).
Stratégie
Pour construire une équation de la forme \(a x + b y + c = 0\), on part d'un point \(M (x;y)\) quelconque de la droite.
L'idée de la preuve est de remarque que les vecteurs \(\vec{AM}\) et \(\vec{u}\) sont colinéaires (voir schéma ci-dessous).

Utilisation de la condition de colinéarité \(x y' - x' y = 0\)
Soit \(M (x;y)\) un point de la droite \((D)\).
Le vecteur \(\vec{AM}\begin{pmatrix} x - x_A \\ y - y_A \\ \end{pmatrix}\) est un vecteur directeur de \((D)\) (de même que \(\vec{u}\))
Donc \(\vec{u}\) et \(\vec{AM}\) sont colinéaires
Donc en appliquant la formule analytique : $$ \begin{array}{lll} (x-x_A)\times \beta - \alpha (y-y_A) &=& 0\\ \beta x - \beta x_A - \alpha y+\alpha y_A &=& 0\\ \beta x + \alpha y + (\alpha y_A - \beta x_A) &=& 0 \end{array} $$
Conclusion
On obtient une équation cartésienne \((D):a x + b y + c = 0\) avec \(a = \beta\), \(b = \alpha\) et \(c=\alpha y_A - \beta x_A\). De plus \(\beta\) et \(\alpha\) ne sont pas tous les deux nuls car \(\vec{u}\begin{pmatrix} \alpha \\ \beta \\ \end{pmatrix}\neq\vec{0}\)
Exercice type : trouver une équation cartésienne de droiteSoient \(D\) une droite ayant pour vecteur directeur \(\vec{u}\begin{pmatrix} 1 \\ -2 \\ \end{pmatrix}\) et passant par le point \(A (1;3)\). Déterminer une équation cartésienne de la droite \((D)\). |

|
Soit \(M (x;y)\) un point de la droite \((D)\).
Le vecteur \(\vec{AM}\begin{pmatrix} x - 1 \\ y - 3 \\ \end{pmatrix}\) est un vecteur directeur de \((D)\) (de même que \(\vec{u}\))
Donc \(\vec{u}\) et \(\vec{AM}\) sont colinéaires
Donc en appliquant la formule analytique : $$ \begin{array}{lll} (x-1)\times (-2) - 1 (y-3) &=& 0\\ -2 x+2 - y+3 &=& 0\\ -2 x-y+5 &=& 0 \end{array} $$
En conclusion \((D):-2 x - y + 5 = 0\)